Parallel Diffusion vs Sequential Dijkstra

Both the parallel diffusion and sequential dijkstra implementations have been run on a range of 6 different maps. In each case the time to find a path and the number of nodes in the path have been recorded.

Each map is made up for a 32x32 grid where each tile has a varying terrain cost associated with it. In each case the source node is the top left corner and the goal node is the bottom left.

Map 1

Map 1 was the simplest of the maps containing no obstacles or costly terrain. In both the diffusion and dijkstra applications each found the same path; which in this case was to simply move directly from the start to the goal with a path length of 32 nodes. However diffusion was able to do this approximately 80% quicker taking only 0.18ms compared to 0.97ms for dijkstra.

Diffusion Path

Dijkstra path

Map 2

Map 2 contains some more obstacles and varying terrain we have a small 'beach' with a lake in the middle and river with a bridge in the centre. 

Of all the maps that were tested this provided the greatest variant in path length between the two implementations. Surprisingly the diffusion implementation found a shorter path traversing only 39 nodes to reach the destination compared to the 49 taken by dijkstra. The reason for this is that the diffusion implementation chooses to move over the terrain by walking across the beach and going straight through the river whereas dijkstra chooses to take the bridge across and avoid getting wet. 

Again diffusion was able to find the path quicker taking only 0.23ms compared to 1.01ms for dijkstra.

72.2% of people asked felt that diffusion provided a more realistic path compared to dijkstra

Diffusion Path

Dijkstra Path

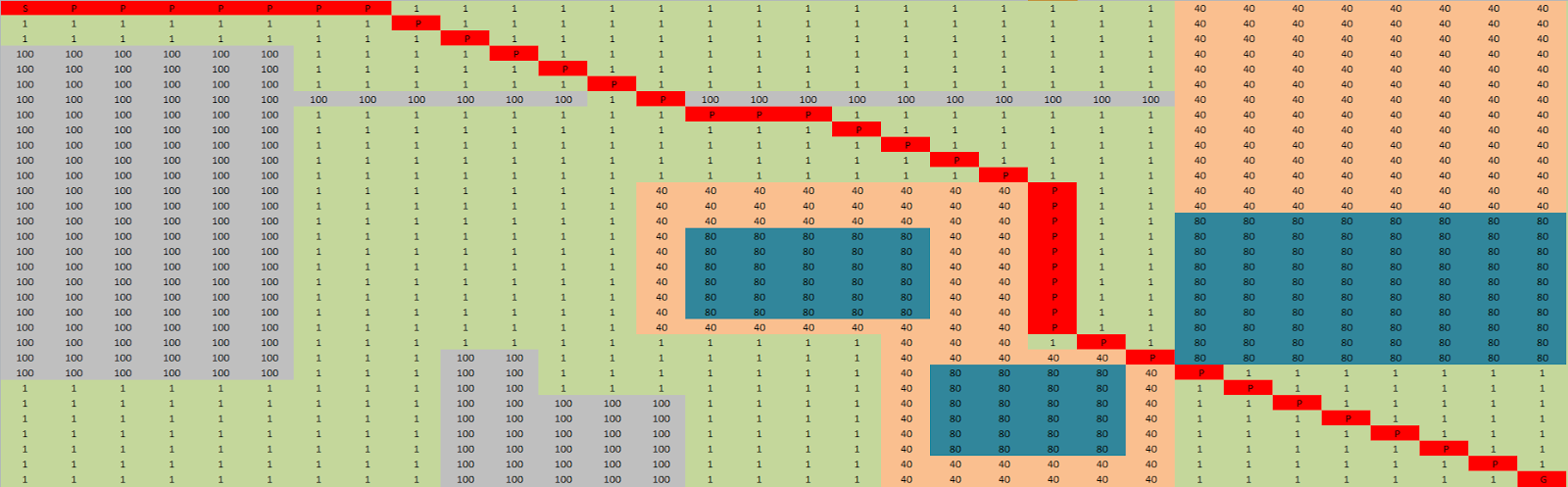
Map 3

Map 3 adds some more terrain and obstacles to the map covering approximately 50% of all the nodes.

Diffusion was able to find the shorter path again by choosing to walk across the beach in the centre to reach the goal, whereas dijkstra choose to avoid it resulting in a longer path traversing 41 nodes compared to diffusions 38.

Diffusion was also able to find the path quicker taking only 0.22ms compared to 1.05ms for dijkstra.

72.2% of people asked felt that diffusion provided a more realistic path compared to dijkstra

Diffusion Path

Dijkstra Path

Map 4

Map 4 was the most complex of all the maps that were tested providing a maze like structure for the implementations to solve. Interestingly both were able to find pretty much the same path traversing 61 nodes to reach the goal. 

In this example dijkstra was actually able to find the path quicker than diffusion, however this is believed to be down to the specific implementation of diffusion.

66.7% of people asked felt that dijkstra provided a more realistic path compared to diffusion

Diffusion Path

Dijkstra Path

Map 5

In map 5 we test what happens when the goal is inaccessible. In both cases a path could not be found from the start to the goal. Interestingly again dijkstra was able to find that no path exists quicker than diffusion, however this is due to the nature of the diffusion implementation itself. 

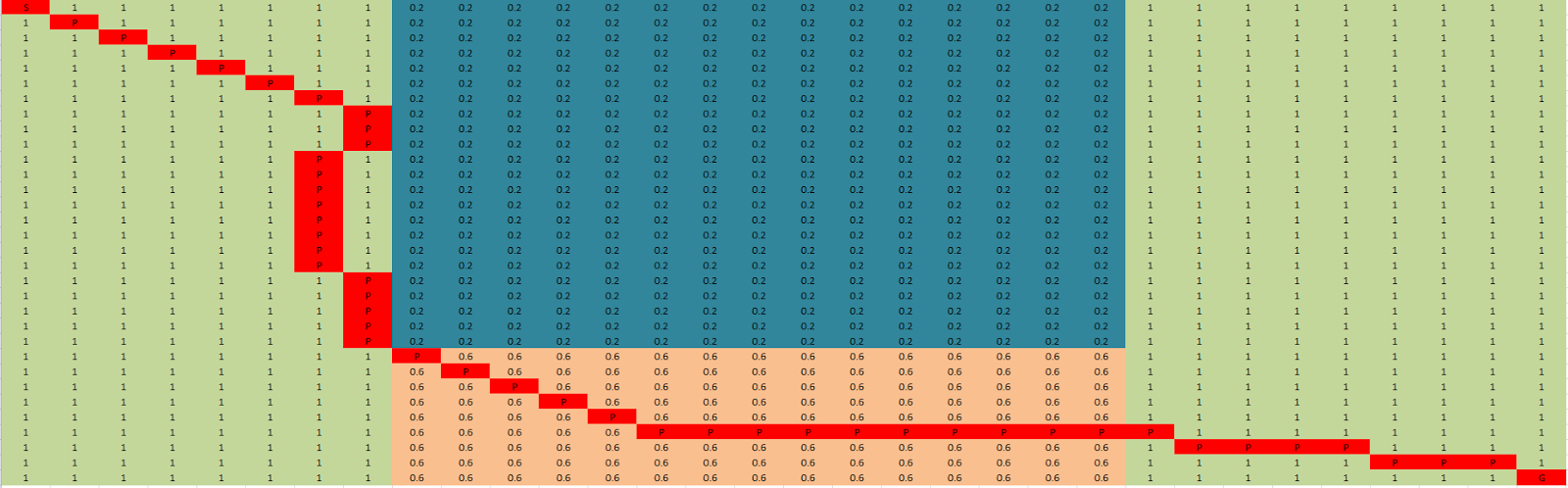
Map 6

In map 6 we test what happens when we must move through a set of terrain.

Both diffusion and dijkstra chose to move over the less costly of the two terrain options and both found a path in which they traverse 47 nodes to reach the goal, however looking at the images below we can see they actually take very different paths.

Diffusion was able to find a path quicker taking only 0.18ms compare to 0.95ms for dijkstra.

50% of people asked felt that diffusion provided a more realistic path compared to dijkstra

diffusion path

dijkstra path